| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- hypergraph
- LIIF
- Reference-based SR
- Referense Super Resoltuion
- SegFormer
- INR
- DIINN
- Reference Super-Resolution
- ADE20K
- deep learning
- arbitrary scale
- Cityscapes
- Super-Resolution
- Cell-tissue
- SISR
- ConvNeXt
- FRFSR
- TRANSFORMER
- graph neural network
- CrossNet
- implicit representation
- Cell detection
- Feature reuse
- Tissue segmentation
- GNN in image
- Zero-Shot sr
- GNN
- Graph
- session-based recommendation
- TAAM
- Today
- Total
딥러닝 분석가 가리
Graph Neural Network in Image (2) 본문
https://dlgari33.tistory.com/13
이번 포스팅은 Spatial-based ConvGNNs을 다루므로 Spectral-based ConvGNNs 내용은 위 블로그 글을 참조하세요!
Spatial-based ConvGNNs
영상에서 CNN과 유사한 convolutional 연산인 spatial-based 방법은 노드들의 공간상의 관계에 기반해 graph convolution을 정의한다. 영상은 각 픽셀이 노드로 나타나는 그래프의 특별한 형태로 고려되어질수 있다. 2D convolution과 graph convolution의 형태는 그림 1과 같다. 2D conv가 중심픽셀로 부터 인접한 픽셀을 kernel로 가중치를 계산하듯 graph conv도 중심 노드로 부터 인접한 노드간의 가중치를 계산할 수 있다. 다른 관점으로는 spatial-based ConvGNN은 RecGNN의 information propagation 이나 message passing과의 같은 개념으로 볼 수 있다. 즉, spatial graph convolution operation은 node 정보를 edge를 따라 전파하는 형식이다.

Neural Network for Graphs (NN4G)
NN4G는 처음으로 spatial-based ConvGNN을 적용했다. NN4G와 RecGNN과의 구별되는 차이점은 NN4G는 각 layer의 독립적인 parameters를 가진 compositional neural architecture를 통해서 graph 간의 상호 의존성을 배우는 것이다. 인접 노드들은 점증법(incremental construction) 구조를 통해 확장될 수 있어, NN4G는 인접 노드간의 정보를 직접적으로 합하는것으로 graph convolution을 수행한다. NN4G는 또한 residual connection과 skip connection을 적용해 각 layer 마다 memorize 정보를 전파한다. 그 결과 NN4G는 다음 layer의 노드 상태를 도출하고 이에 대한 식은 식 1과 같고, 식 1의 h_v ^{(0)} = 0 이라고 정의하면 식 2로 정의된다.

이는 GCN과 닮았는데, 차이가 있다면 NN4G는 hidden node의 상태가 극도로 다른 scale이 될수도 있는 unnormalized adjacency matrix를 사용한다는것이다. NN4G에 영감을 받아 제안된 확률기반의 모델인 CGMM(Contextual Graph Markov Model)은 확률적으로 해석이 가능하다는 장점이 있다.
Diffusion Convolutional Neural Network (DCNN)
DCNN은 graph convolution을 diffusion process(확산 과정)로 간주한다. Diffusion process는 정보 분포가 여러 rounds를 거친 후 동일한 상태에 도달할수 있도록 특정한 전히 확률로 한 노드에서 이웃 노드 중 하나로 정보가 전송된다고 가정한다. DCNN은 diffusion graph convolution으로 정의된다.

f(·)는 활성화 함수, 확률 전이 행렬 P ∈ R^{n×n}는 P = D^{-1} A로 계산된다. DCNN의 hidden representation matrix H^(k)는 입력 feature matrix X와 같은 차원이며 이전의 hidden representation matrix H^(k-1)의 함수가 아니다. DCNN은 최종 출력을 모든 H를 연결해 사용한다. 반면, 연결대신 sum 연산을 사용하는 DGC(Diffusion Graph Convolution)도 있다. DGC는 식 4와 같이 정의된다. W^(k) ∈ R^{D×F} 이고, f(·)는 활성화 함수이다.

PCG-DGCNN
Transition probability matrix의 힘을 사용하는것은 먼 이웃이 중앙 node에 정보를 거의 제공하지 않는다는것을 의미한다. PCG-DGCNN은 최단 경로를 기준으로해 먼 이웃의 기여를 증가시킨다. 짧은 경로의 인접 행렬을 S^(j)로 정의하고, 만약 node v에서 u 까지가 최단 경로 j 라면, S_v,u ^{j} = 1이거나 0으로 한다. PGC-DGCNN은 receptive field 크기를 조정하는 하이퍼 파라미터 r이 있다. PGC-DGCNN의 graph convolutional 연산은 식 5와 같이 나타낼 수 있다.

|| 는 vetctor의 concat을 나타낸다. 최단 경로의 인접행렬의 계산은 시간복잡도가 최대 O(n^3)가 될 수 있다. PCG-DGCNN은 receptive field의 크기에 따라 중심 노드로 부터 멀리 있는 노드도 같이 고려하여 먼 이웃의 기여를 증가시킬 수 있다.
Partition Graph Convolution (PGC)
PGC는 최단 경로에 제한되지 않는 특정한 기준에 따라 인접 노드를 Q 그룹으로 나누고 각 그룹별로 정의된 이웃에 따라 Q 개의 인접 행렬을 정의한다. 그리고 나서 PCG는 다른 parameter matrix를 가진 GCN을 각 인접 그룹에 적용하고 결과들을 합해준다. 이에 따른 식은 식 6과 같다.

식 6의 각 의미는 아래와 같다.

Message Passing Neural Network (MPNN)
MPNN은 spatial-based ConvGNNs의 일반적인 framework를 설명한다. MPNN은 정보가 직접적으로 한 node 에서 다른 edge로 전파될 수 있는 message passing process를 graph convolutoin으로 다룬다. MPNN은 정보가 더 전파되도록 하기 위해 message passing을 k 번 반복한다. Spatial graph convolution인 message passing function은 다음과 같이 정의 된다.

h_v^{(0)}은 x_v 이고, U_k(·), M_k(·)은 학습 가능한 매개변수를 가진 함수이다. 각 노드의 hidden representation이 계산된 후에, h_v^{(K)}는 node-level 예측을 수행하기위해 출력 layer로 전파되거나 graph-level 예측을 수행하기 위한 읽기 함수(readout function)로 전달될 수 있다. Readout function은 node의 숨겨진 표현을 바탕으로 전체 그래프의 표현을 생성한다. 그리고 이것은 일반적으로 식 8과 같이 정의된다.

R(·)는 학습가능한 파라미터를 가진 readout function이다. MPNN은 U_k(·), M_k(·), R(·)를 다른 형태로 나타내 다른 GNN에 적용할 수 있다. 하지만, GIN(Graph Isomorphism Network)은 이전의 MPNN 기반의 방법이 생성된 그래프 임베딩을 기반으로 하므로 서로 다른 그래프 구조를 구별할 수 없다는것을 발견하고, 이 단점을 수정하기 위해 학습 가능한 파라미터의 중심 노드의 weight를 조정한다. Graph convolution의 수행 식은 식 9와 같다.

GraphSage
인접한 노드의 수는 한개에서 1천개 혹은 그 이상으로 매우 다양한데, 이 노드들을 전부 다 계산하는것은 비효율 적이다. 그래서 GraphSage는 각 노드마다 고정된 수 만큼의 인접 노드를 얻기 위해 sampling을 사용한다. GraphSage의 수식은 식 10과 같다.

여기서 h_v^{(0)}은 x_v 이고, f_k(·)는 agrregation function이다. S_{N(v)}는 노드 v의 인접 노드를 random sample한다. Aggregation function은 평균, 합, 최대 함수의 값들은 노드 순서가 변하더라도 값은 변하지 않아야 한다.
Graph Attention Network (GAT)
GAT는 중앙 노드와 인접한 노드의 기여도를 추정하는 방법이 인접 노드의 샘플을 추출하는 GraphSage나 미리 정의된 GCN과는 다르다. 이 차이점은 그림 2에 나타난다. GAT는 attention 방법을 사용해 연결된 두 노드간의 상대적인 가중치를 학습한다. GAT의 grap convolutoin 연산은 식 11과 같이 나타낼 수 있다.


h_v^{(0)}는 x_v 이고, Attention weight는 두 노드간의 연결 강도를 측정한다. 그래서 두 노드 v, u간의 attention 식은 식 12와 같다.
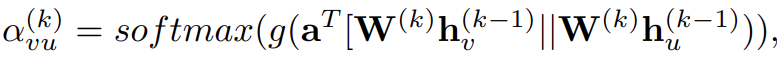
g(·)는 LearkyReLU이고, a는 학습가능한 매개변수 vector 이다. Softmax 함수는 노드 v의 모든 인접노드의 attention weights의 합계가 1이라는 것을 보장한다. 게다가 GAT는 multi-head attention으로 모델의 표현 능력을 향상 시킨다. GAT가 attention head간의 기여를 동일하게 계산할때, GAAN (Gated Attention Network)는 각 attention head 마다 추가적인 attention score를 계산해주는 self-attention mechanism을 도입한다. GeniePath는 graph convolutoin layer간의 정보 흐름을 통제하기 위해 LSTM 같은 gating mechanism을 제안한다. 다른 graph attention model도 많지만, ConvGNN framework에 속하지 않는다. (어떤 모델들이 속하지 않는지를 알아보려면 논문의 인용번호 88, 89번을 보는것이 좋을듯 하다.)
Mixture Model Network (MoNet)
MoNet은 인접 노드간의 다른 가중치를 주기위해 다른 방법을 사용한다. MoNet은 노드와 인접 노드간의 상대적인 위치를 결정하기 위해 pseudo-coordinate(유사좌표) 노드를 도입한다. 두 노드간의 상대적인 위치가 알려지면, weight function은 두 노드 간의 위치에 맞는 가중치를 매핑한다. 이 방법으로, graph filter의 매개변수는 다른 위치에도 공유될 수 있다. MoNet framework에서 존재하는 manifold와 같은 몇가지 방법, Geodesic CNN(GCNN), Anisotropic CNN (ACNN), Spline CNN, 그리고 그래프 같은 GCN, DCNN은 nonparametric weight funcion을 구성해 MoNet의 특별한 instance로 일반화 할 수 있다. MoNet은 추가적으로 adaptive하게 weight function을 배우기 위해학습 가능한 매개변수를 가진 Gaussian kernel을 처리한다.
PATCHY-SAN
PATCHY-SAN은 graph labeling에 따라 각 노드의 이웃을 정렬하고 상위 q 이웃을 선택한다. Graph labelings은 기본적으로 node degree, centrality, 그리고 Weisfeiler Lehman 색상을 도출할 수 있는 node 점수이다. 이제 각 노드에 고정된 수의 정렬된 인접 노드가 있어 graph-structured 데이터를 grid-structured 데이터로 변환할 수 있다. PATCHY-SAN은 인접한 feature 정보를 집계하기 위해 1D conv를 적용한다. 이때, 필터의 가중치 순서는 노드의 인접 순서에 해당한다. PATCHY-SAN은 ranking 기준이 graph structure에만 적용되고 데이터를 처리하기 위해 연산량이 많이 요구된다는 단점이 있다.
Large-scale Graph Convolutional Network (LGCN)
LGCN은 노드의 feature 정보를 기준으로해 인접 노드의 순위를 정한다. LGCN의 각 노드는 feature matrix를 모은다. Feature matrix는 이것의 이웃으로 구성되고 각 column을 따라 정렬된다. 그리고 상위 q 개의 중심 노드를 입력으로 사용한다.
Paper
https://arxiv.org/pdf/1901.00596.pdf
'딥러닝 논문 리뷰' 카테고리의 다른 글
| Adversarial Text Image Super-Resolution Using Sinkhorn Distance Review (1) | 2023.04.20 |
|---|---|
| Graph Neural Network in Image (3) (0) | 2023.04.19 |
| Graph Neural Network in Image (1) (0) | 2023.04.02 |
| IGNN(Internal Graph Neural Network) Image Super-Resolution Review (0) | 2023.03.29 |
| Activating More Pixels in Image Super-Resolution Transformer Review (0) | 2023.03.11 |




