| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- ConvNeXt
- deep learning
- ADE20K
- GNN in image
- Zero-Shot sr
- SISR
- DIINN
- INR
- TRANSFORMER
- LIIF
- hypergraph
- session-based recommendation
- Reference Super-Resolution
- GNN
- Cell detection
- Referense Super Resoltuion
- SegFormer
- graph neural network
- Cityscapes
- arbitrary scale
- Cell-tissue
- implicit representation
- Super-Resolution
- FRFSR
- TAAM
- Tissue segmentation
- CrossNet
- Graph
- Feature reuse
- Reference-based SR
- Today
- Total
딥러닝 분석가 가리
Graph Neural Network in Image (1) 본문
Graph and Tree
데이터는 euclidean data와 non-euclidean data로 나눌수 있는데 이때, non-euclidean data는 graph나 tree 구조를 가진 데이터이다. Graph는 연결된 edge들이 방향성이 있거나 없는 순환되는 구조, tree는 방향성이 있는 그래프의 종류, 단, tree는 root node가 하나로 고정되어있다. Graph와 Tree의 구조는 그림 1과 같다.

A Comprehensive Survey on Graph Neural Networks
https://arxiv.org/pdf/1901.00596.pdf 에서는 Graph를 총 4가지 RecGNN(Recurrent Graph Neural Network), ConvGNN (Convolutional GNN), GAE(Graph AutoEncoer), STGNN(Spatial-Temporal GNN)으로 나눈다. 이중 주로 이미지를 처리하는 graph는 ConvGNN으로 CNN이 computer vision 영역에서 좋은 성과를 보여 convolution을 graph로 재 정의한 분야이다. ConvGNN은 spectral-based와 spatial-based 두가지로 나뉜다. Spectral-based는 고유값과 고유 벡터를 이용해 분석하는 spectral graph 이론에 기반하여 만들어진것이고, Spatial-based는 RecGNN에서 메시지 전달에 대한 아이디어를 상속하며 구조적으로 복합적인 non-recursive layers에 의한 그래프 상호 의존성을 처음 다루었다.
Convolutional Graph Neural Networks
ConvGNNs은 RecGNNs과 밀접하게 관련이 있다. ConvGNNs는 contractive 제약 조건으로 노드 상태를 반복하는 대신에, 구조적으로 각 layer의 가중치가 서로 다른 고정된 수의 layer를 사용해 순환적 상호 의존성을 다룬다. ConvGNN은 spectral과 spatial 두가지로 나뉜다. Spectral 기반의 접근은 그래프 신호 처리 관점으로 부터의 필터로 소개되는 graph convolution으로 정의한다. Graph convolution 연산은 그래프 신호로 노이즈를 제거하는 것으로 해석된다. Spatial 기반의 접근은 RecGNN에 아이디어를 상속해 정보를 전파에 의한 graph convolution을 정의한다. GCN이 두 기법의 차이를 메운 뒤, spatial-based는 급격하게 최근까지 효율적이게 유용하게 일반적이게 발전되었다.
Spatial-based ConvGNNs은 다음 글에서 정리했으니 찾아 보도록 하자!
https://dlgari33.tistory.com/14
Spectral-based ConvGNNs
Background - Laplacian operator
Laplacian operator는 Divergence of Gradient이다. 영상에서는 Laplacian filiter를 사용하게 되면 영상 내에서 전경과 배경의 구분 혹은 전경과 전경의 구분 등의 경계선에서 필터의 결과값이 균일하지 않은곳은 Laplacian 값이 크게나와 영상의 edge를 검출할 수 있다. 이 내용으로 graph에 Laplacian operator를 사용하면 영상에서 전경과 배경의 차이를 나타내듯이, 각 노드와 이웃 노드 간의 차이를 나타낼 수 있다. Laplacian matrix는 수학적표현으로 무방향 그래프이며, L = D - A로 나타낼수 있다. D는 노드의 차수인 대각행렬이고, A는 인접행렬을 의미한다. Laplacian matrix는 real symmetric positive semidefinite(실수 대칭 양의 반정형)의 속성을 가지고 있어 L = UΛU^T 로 나타낼 수 있다. 즉, Laplacian matrix를 고윳값 분해를 하면 전과 같은 식을 유도할 수 있다. 이때 U 는 고유값의 순서로 정렬된 고유벡터 Λ는 고유값의 대각행렬이다. Spectral-based mehtod는 graph를 무방향으로 가정하는데, normalized graph Laplacican matrix는 무방향 그래프로 표현할 수 있으므로 L = D - A를 다음 식과 같이 나타낼 수도 있다.

Background - Fourier transform
Fourier transform은 시간 영역에서 표현된 신호를 주파수 영역으로 변호나해주는 것으로, 영상처리에서는 축 방향으로 따라가며 픽셀의 밝기 변화를 신호로 보고 주파수를 분석하는것이다. 푸리에 변환의 기본 개념은 하나의 신호는 여러 개의 sin 신호와 cos신호의 합으로 표현할 수 있다 이므로, 두 주파수의 성분을 파악해 신호를 분석한다. 즉, 그래프를 표현하는 어떤 신호가 존재할 때, 이를 어떤 함수들의 합으로 표현하자는 것이다. 그래프 푸리에 변환에서 신호 x를 식으로 정의하면 아래 식과 같다.

x hat은 graph fourier transform으로 부터 나온 신호의 결과를 나타낸다. 그래프 푸리에 변환은 normalized graph Laplacian의 고유벡터에 의해 basis가 형성되는 orthonormal space에 입력 그래프 신호를 투영한다. 변환된 신호 x hat의 요소는 새로운 공간에서 그래프 신호의 좌표 이므로 입력 신호는 아래 식처럼 나타낼 수 있다. 이 식은 정확히 inverse graph Fourier transform 이다.

이 식을 다시 입력 신호 x 와 filter g ∈ R^n의 graph convolution으로 정의하면 아래 식과 같다.

⊙는 element-wise product를 의미한다. 만약 위 식에서 filter를 gθ = diag(U^T g)로 정의 한다면 spectral graph convolution은 다음 식과 같이 간단해질 수 있다.

Spectral-based ConvGNNs
Laplacian operator과 Fourier Transform에 따른 Spectral-based ConvGNNs은 다음과 같은 흐름이 있다.
- Spectral-based ConvGNN은 신호처리에서 사용하는 Fourier transform을 활용해 convolution 이론과 연결해 사용함
- Fourier transform을 위해 Laplacian operator을 사용함 (normalized garph Laplacian matrix)
- Graph Laplacian operator은 두 노드간의 거리를 나타내는 방법
- Laplacian matrix에 고윳값 분해를 사용해 고윳값 과 고유벡터를 활용
- Fourier transform에 사용하는 고유벡터를 Laplacian matrix에서 구한 고유벡터로 사용
Spectral-based ConvGNN은 위의 정의들을 따르며 filter에 따라 차이가 있다. Spectral-based ConvGNNs은 필터가 학습 가능한 파라미터라고 가정하며 여러 채널이 있는 그래프 신호를 고려한다. Spectral CNN의 graph convolutional layer는 다음과 같이 정의할 수 있다. 즉, 아래 식을 통해 convolution 연산을 한다.

k 는 layer index, H^(k-1) ∈ R^(n×f_(k−1))는 입력 graph 신호, H^(0)은 X, f_(k-1)은 입력 채널의 수 그리고 f_k는 출력 채널의 수, Θ^(k)는 학습 파라미터로 채워진 단위 행렬이다. Laplacian matrix의 고유값 분해 때문에 Spectral CNN은 3가지 단점이 있다.
- 그래프에 대한 perturbation(동요, 섭동)은 eigenbasis(고유편향)의 변화를 가져옴
- 학습된 필터는 도메인에 의존하며 이는 다른 구조를 가진 그래프에 적용할 수가 없음
- 고유값 분해는 O(n^3)의 계산 복잡도를 요구함
이러한 점에 따라 ChebNet과 GCN은 몇가지 근사치와 단순화를 통해 계산 복잡도를 O(m)으로 줄였다.
Chebyshev Spectral CNN (ChebNet)
ChebNet은 필터를 Chebyshev polynomial of the diagnoal matrix of eigenvalues로 근사한것이다. 이에 따른 필터는 아래와 같이 정의된다.

Chebyshev polynomials을 재귀적으로 정의하면 다음과 같이 나타낼 수 있다. 이때 T_0(x)는 1, T_1(x)는 x 이다.

Graph 신호 x에 대한 convoltuion, 즉 식 7을 식 5에 적용하면 다음 식으로 정의 할 수 있다.

그리고 다음 식 10에 의해 식 9를 식 11처럼 표현할 수 있다.


Spectral CNN에 대한 개선으로 ChebNet에 의해 정의된 filter는 공간산에 존재한다. 즉, 필터가 그래프 크기와는 독립적으로 local feature를 추출 할 수 있다. ChebNet의 spectrum은 -1 부터 1까지, [-1, 1], 선형적으로 map 되어진다. CayleyNet은 주파수의 좁은 대역폭을 capture하기 위한 매개변수의 rational complex 함수인 Cayley polynomials을 적용한다. CayleyNet의 spectral graph convolution은 다음과 같이 정의 된다.

Re(·) 는 complex number의 real part를 반환, c_o 는 real coefficent, c_j 는 complex coefficent, i 는 imaginary number(허수), 그리고 h 는 Cayley filter의 spectrum을 조절하는 매개변수 이다. CayleyNet은 공간적 인접성을 보존하며 ChebNet이 CayleyNet의 특별한 경우로 간주 되어 질 수 있음을 보여준다.
Graph Convolutional Network (GCN)
GCN은 ChebNet의 첫번째 근사로 나타낼수 있다. K = 1, λ_{max} = 2 라고 할때, 식 11을 다음 식 13과 같이 간소화 할 수 있다.
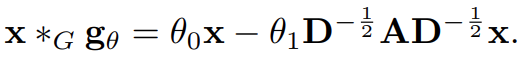
매개변수의 수를 억제하고 과적합을 피하기 위해 GCN은 θ = θ_0 = −θ_1 라고 가정하면 다음과 같이 정의된 graph convolution을 식 14와 같이 나타낼 수 있다. 입력과 출력의 다중 channel을 허락한다면, GCN은 식 14를 compositional layer로 수정하고 식 15로 정의할 수 있다.

여기서 A bar는 numerical instability를 해결하기 위해 normalization trick를 적용시켜 아래와 같이 나타낸다.

Spectral-based method인 GCN은 spatial-baed method로 해석할 수 있다. Spatial-based 관점에서 GCN은 인접 노드로 부터 feature 정보를 aggregation하는것을 볼수 있기 때문이다. 그래서 식 15는 다음 식 16처럼 표현될수 있다.

Adaptive Graph Convolutional Network (AGCN)
AGCN은 그래프 인접 행렬에 표현되지 않은 숨은 구조적 관계를 학습한다. 이것은 두 노드의 feature를 입력으로 하는 학습 가능한 distance function을 통해 'residual graph adjacency matrix'라고 불리는것을 구성한다.
Dual Graph Convolutional Network (DGCN)
DGCN은 dual graph convolutional 구조로 두개의 graph convolutional layer를 parallel 하게 학습한다. 두 layer의 매개변수를 공유하는 동안, normalized adjacency matrix와 PPMI(Positive Pointwise Mutual Information) matrix를 사용한다. PPMI는 graph로 부터 sample된 random walks를 통해 노드 간의 co-occurrence(동시 발생) 정보를 catpure한다. PPMI 행렬은 다음과 같이 정의된다. Random walk는 무작위로 움직이는것으로, 그래프로 정의하면 주어진 그래프에서 정의한 node와 edge의 특성에 맞춰 무작위로 sequence를 만드는것이다.

v1, v2 ∈ V, |D| = ∑_{v1,v2} count(v1, v2), count(·)는 node v와 node u로 부터 발생한 빈도수를 계산하는 함수이다. Dual graph convolution layer로 부터 나온 출력을 ensemble하는 DGCN은 graph convolutional layer를 깊게 쌓지 않아도 local, global structural 정보를 encode 할 수 있다.
Paper
https://arxiv.org/pdf/1901.00596.pdf
'딥러닝 논문 리뷰' 카테고리의 다른 글
| Graph Neural Network in Image (3) (0) | 2023.04.19 |
|---|---|
| Graph Neural Network in Image (2) (0) | 2023.04.05 |
| IGNN(Internal Graph Neural Network) Image Super-Resolution Review (0) | 2023.03.29 |
| Activating More Pixels in Image Super-Resolution Transformer Review (0) | 2023.03.11 |
| CSPNet Review (1) | 2023.03.02 |




